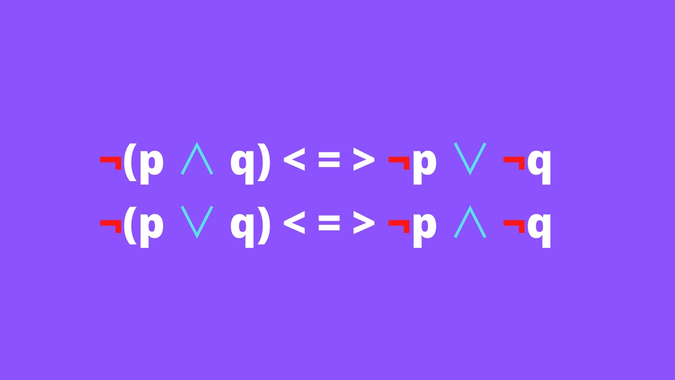
Logic Laws (Part 1)

We can use logical laws to reduce complex formulas into simpler ones.

Here we should add to new symbols:

1. T : Tautology (always 1)
2. F : Contradiction (always 0)

Because of this previously we avoided using T for True and F for False.

There are several laws that make our job easy in Logic:

• 1) Identity law

It says that if you will have the situation where proposition AND Tautology the result depends on proposition. The same is true for proposition OR Contradiction.

• 2) Domination Law

Domination law says "If proposition OR Tautology then Tautology is the result" and "If proposition AND Contradiction then Contradiction is the result".

• 3) Double Negation Law

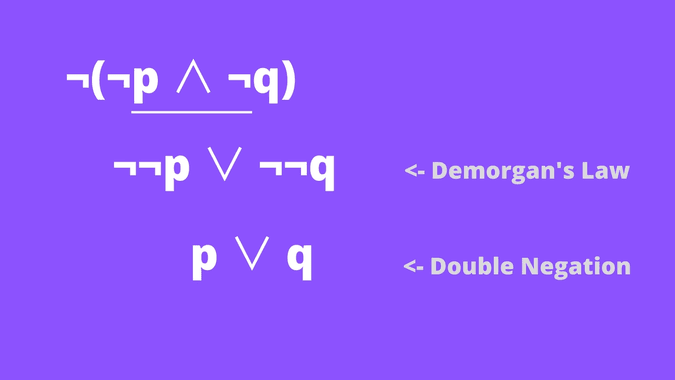
I think the picture speaks for itself. It is clear that "not not raining" means that "It is raining".

• 4) DeMorMorgan's Law

I think this law is the most important among others, since it is so wildly used.

This law is basically for getting propositions out of the parenthesis.

🔵We will finish this part with the example for Double Negation and DeMorgan's Law.

Written by Asadulloh Rakhimov